MATEMATIKA PEMINATAN KELAS 12


 Limit

Limit, secara bahasa dapat diartikan sebagai ambang batas. Misalnya, sebuah kartu kredit memiliki limit Rp5.000.000,00. Artinya, kartu kredit tersebut mempunyai ambang batas Rp5.000.000,00. Begitu juga untuk pengertian limit secara matematika, limit dalam matematika juga dapat diartikan sebagai batas yang dapat dicapai di suatu titik. Melalui halaman ini, idschool akan mengulas tentang pengertian limit.
Dalam matematika, limit dapat dikatakan sebagai prediksi nilai ordinat yang didapat pada suatu titik. Nilai limit diperoleh dengan pendekatan dari sisi kanan dan sisi kiri. Jika nilai limit dari kiri sama dengan nilai limit dari kanan maka fungsi f(x) mempunyai nilai limit. Notasi limit dismibolkan pada persamaan di bawah.
Pengertian limit
Cara membaca notasi limit di atas adalah nilai limit f(x) untuk x mendekati a dinyatakan dalam sebuah nilai yang terletak pada ordinat (y). Secara baku, limit dinyatakan melalui definisi di bawah.
Penjelasan mengenai limit untuk lebih detailnya akan diberikan melalui beberapa kasus yang akan diberikan di bawah.

Nilai Limit Terdefinisi di Semua Titik

Bagaimana cara mencari nilai limit?
Nilai limit diperoleh melalui pendekatan dari kiri dan kanan. Secara sederhana, limit dapat diartikan sebagai nilai y yang merupakan prediksi dari nilai suatu fungsi di suatu titik.
Ulasan pertama yang akan dibahas adalah menentukan nilai limit pada grafik linear. Seperti kita tahu bahwa grafik linear terdefinisi di semua titik. Perhatikan grafik fungsi linear di bawah.
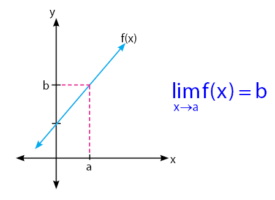
pengertian limit fungsi
Berdasarkan grafik di atas, nilai x terdefinisi di semua titik. Nilai limit f(x) untuk x mendekati a dari kanan adalah b dan nilai limit f(x) untuk x mendektai a dari kiri adalah b. Sehingga, kesimpulan yang dapat diambil adalah nilai limit f(x) adalah b.
Contoh kasus pertama ini merupakan kasus sederhana tentang limit karena diberikan grafik linear yang nilai x terdefinisi di semua titik
Pada pembahasan limit, kita tidak melihat apa yang terjadi pada satu titik, tapi melihat nilai yang dapat terjadi di sekitar titik ketika didekati sangat dekat dari kiri dan dari kanan. Kondisi tertentu dapat memungkinkan grafik yang nilai x tidak terdefinisi di suatu titik. Namun, tidak mustahil jika nilai limitnya sama dengan grafik yang terdefinisi di semua titik.
Untuk lebih jelasnya, perhatikan grafik yang diberikan pada gambar di bawah.
nilai limit fungsi
Grafik di atas tidak terdefinisi pada titik x = a. Namun, ketika fungsi f(x) didekati dari kiri, nilainya akan menuju titik b. Begitu juga ketika f(x) didekati dari kanan, nilainya akan menuju titik b. Kesimpulannya, nilai limit f(x) adalah b.
pengertian limit fungsi
Sebagian orang mungkin menanyakan, mengapa jika nilai limit merupakan nilai yang diperoleh dari pendekataan, notasi limit disimbolkan dengan tanda sama dengan?
Hal ini dikarenakan penyimbolan limit memang dibuat seperti demikian. Ini merupakan simbol notasi limit, tidak ada alasan lain.

Nilai Limit Tidak Ada

Ada sebuah kondisi tertentu, di mana nilai limit f(x) yang didekati dari kiri tidak sama dengan nilai limit yang didekati dari kanan. Kondisi ini tentunya tidak akan menghasilkan nilai limit. Untuk lebih jelasnya, perhatikan grafik di bawah.
limit fungsi
Untuk mendapatkan nilai limit f(x) di titik x = a, sobat idschool perlu mencari tahu nilai limit f(x) jika x didekati dari kiri dan kanan. Selanjutnya, sobat idschool perlu membandingkan nilai limit f(x) untuk x mendekati a dari kiri dan untuk x mendekati a dari kanan.
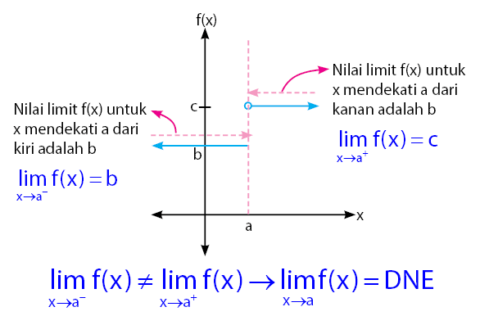
limit fungsi nilia mutlak
Berdasarkan grafik yang diberikan di atas, untuk x mendekati a dari kiri, nilai limitnya adalah b, sedangkan untuk x mendekati a dari kanan, nilai limitnya adalah c.
Kita mendapatkan nilai limit f(x) untuk x mendekati a dari kiri tidak sama dengan nilai limit f(x) untuk x mendekati a dari kanan. Kesimpulanya, nilai limit f(x) tidak ada, biasa ditulis dengan DNE (Do Not Exist).
Selanjutnya, ulasan kasus yang ke tiga adalah nilai limit untuk x mendekati tak hingga (x \rightarrow \inf) dan x mendekati negatif tak hingga (x \rightarrow - \inf).

Nilai Limit di Tak Hingga

Ulasan yang akan dibahas di sini adalah cara menentukan nilai limit fungsi jika x mendekati tak hingga. Untuk mengetahui caranya, perhatikan gambar grafik fungsi f(x) dan g(x) yang diberikan di bawah.
Nilai Limit Fungsi di Tak Hingga
Nilai limit f(x) untuk x mendekati tak hingga, nilainya adalah 0. Hasil ini diperoleh dengan mendekati nillai f(x) ketika x mendekati tak hingga, grafik akan menuju titik 0. Perhatikan grafik di bawah.
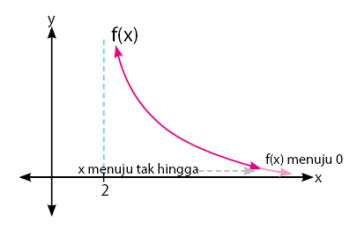
Nilai limit fungi di tak hingga
Hampir sama seperti cara di atas, nilai limit g(x) untuk x mendekati negatif tak hingga, nilainya adalah -1. Hasil ini diperoleh dengan mendekati nillai f(x) ketika x mendekati negatif tak hingga, grafik akan menuju titik -1. Perhatikan grafik di bawah.
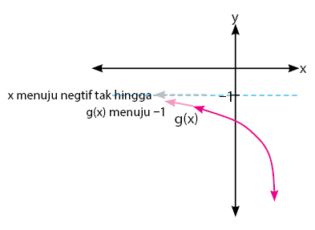
Nilai Limit Fungsi di Tak Hingga

Cara Menentukan Nilai Limit Fungsi Trigonometri

Materi pembahasan limit fungsi trigonometri sebenarnya sama dengan pembahasan materi limit lainnya, seperti pada limit fungsi aljabar. Cara menentukan nilai limit fungsi trigonometri juga tergantung pada nilai x yang mendekatinya. Apakah nilai limit fungsi dengan x mendekati tak hingga atau nilai limit fungsi dengan x mendekati suatu nilai. Bedannya, pada nilai limit trigonometri melibatkan fungsi trigonometri seperti fungsi sin, cos, tan, dan fungsi turunan lainnya.
Sebelum membahas cara menentukan nilai limit fungsi trigonometri, sebaiknya sobat memahami pengertian limit terlebih dahulu. Dengan memahami pengertian limit, akan membantu sobat dalam menyelesaikan soal limit. Baik untuk menentukan nilai limit fungsi trigonometri atau menentukan nilai limit fungsi lainnya.
Variasi soal tentang limit fungsi trigonometri sangat banyak. Ketrampilan menentukan nilai limit fungsi trigonometri akan terasah dengan banyak mengerjakan latihan soal tentang limit fungsi trigonometri. Meskipun soal yang diberikan bervariasi, namun jika sobat sudah menangkap konsepnya maka untuk jenis soal apapun dapat secara mudah untuk diselesaikan. Pada bagian akhir di halaman ini, akan diberikan contoh soal limit fungsi trigonometri yang sudah dilengkapi dengan pembahasan dan teknik rahasia cara menentukan nilai limit fungsi trigonometri.
Selanjunya, mari simak uraian materi pertama yang akan disampaikan yaitu rumus limit fungsi trigonometri untuk x mendekati suatu bilangan.

Limit Fungsi Trigonometri untuk x Mendekati Suatu Bilangan

Cara menentukan nilai limit fungsi trigonometri untuk x mendekati suatu bilangan c dapat secara mudah diperoleh dengan melakukan substitusi nilai c pada fungsi trigonometrinya. Persamaan rumus limit fungsi trigonometri diberikan seperti pada gambar di bawah.
Rumus Limit Fungsi Trigonometri
Berikut ini adalah contoh soal penggunaan rumus limit fungsi trigonometri untuk x mendekati suatu bilangan.
Selesaikan soal limit trigonometri berikut!
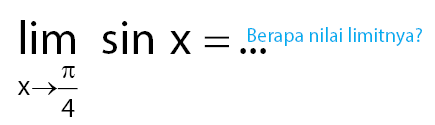
Contoh soal limit fungsi trigonometri
Pembahasan:
Substitusi nilai x = \frac{\pi}{4} pada persamaan fungsi sinus.
    \[ \lim_{x \rightarrow \frac{\pi}{4}} \; sin \; x = sin \; \frac{\pi}{4} \]
    \[ = sin \; 45^{o} \]
    \[ = \frac{1}{2} \sqrt{2} \]
Pada kasus tertentu, nilai limit untuk x mendekati bilangan 0 akan menghasilkan \frac{0}{0}. Misalnya pada kasus berikut.
    \[ \lim_{x \rightarrow 0 } \frac{sin \; x}{x} \]
Jika dilakukan substitusi secara langsung, nilai limitnya adalah
    \[ \lim_{x \rightarrow 0 } \frac{sin \; x}{x} = \frac{0}{0} \]
Sebagaimana yang kita tahu bahwa nilai limit tersebut bukan nilai limit yang diharapkan. Kita perlu menggunakan metode lain untuk mendapatkan nilainya. Sekarang, simak pembahasan selanjutnya mengenai nilai limit fungsi trigonometri untnuk x mendekati 0.

Limit Fungsi Trigonometri untuk x Mendekati 0 (Nol)

Dalam pembahasan limit fungsi trigonometri, terdapat berbagai rumus yang dapat disebut sebagai “properti” untuk menyelesaikan soal limit fungsi trigonometri. Kumpulan properti tersebut dapat dilihat pada daftar rumus limit trigonometri yang diberikan di bawah.
Limit Fungsi Trigonometri
Mungkin, beberapa dari sobat akan bertanya, dari mana properti yang terangkum dalam persamaan di atas diperoleh. Sebenarnya, hasil dari persamaan-persamaan itu diperoleh menggunakan definisi limit dan teorema limit yang sudah ada.
Untuk tingkat Sekolah Menengah Atas, sobat hanya perlu mengetahui properti yang dapat digunakan untuk menyelesaikan soal limit fungsi trigonometri yang ada, seperi yang telah diberikan di atas. Penjelasan dari mana persamaan di atas diperoleh akan diberikan di tingkat lanjut, jika kalian tertarik untuk mengambil matematika sebagai jurusan kuliah sobat
Sekarang, mari kita simak cara menggunakan nilai limit trigonometri menggunakan properti yang diberikan di atas.
Perhatikan soal di bawah!
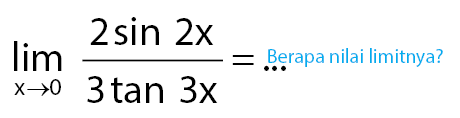
Contoh Soal Limit Fungsi Trigonometri
Pembahasan:
Cara menggunakan properti rumus limit fungsi trigonometri dapat dilihat pada proses pengerjaan mencari nilai limit fungsi trigonometri berikut.
    \[ \lim_{x \rightarrow 0} \frac{2 \cdot sin \; 2x}{3 \cdot tan \; 3x} = \frac{2}{3} \cdot \lim_{x \rightarrow 0} \frac{sin \; 2x}{tan \; 3x} \]
    \[ = \frac{2}{3} \cdot \frac{2}{3} = \frac{4}{9} \]
Dengan mudah, kita dapat mendapatkan nilai limit fungsi trigonometri yang diberikan pada soal adalah \frac{4}{9}.

Komentar

Posting Komentar